Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Suite définie par récurrence
Démonstration par récurrence
Étude des variations et limite
Ressources associées et exercices semblables
Suites liées par une relation de récurrence (ex BAC) (réf 0957)
exercice
Suite définie par une relation de récurrence (réf 0962)
exercice
Suites définies par récurrence (d’après BAC ) (réf 0963)
exercice
- Montrer que pour tout réel $x\in ]0;1[$, on a $0 < x(2-x) < 1$.
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
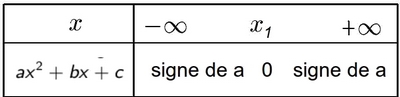
- Cas $\Delta<0$ (aucune racine)
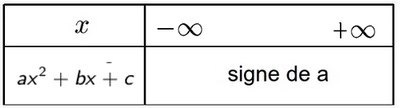
Aide
Pour comprar deux nombres, il faut étudier le signe de leur différence, soit ici $x(2-x)-2$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - En déduire que $0< u_n < 1$ pour tout entier naturel $n$.
Rappel cours
Raisonnement par récurrence
On note $P_n$ une propriété définie pour tout entier naturel $n$.
Initialisation:
$P_0$ est vraie
Hérédité:
Si $P_n$ est vraie alors$P_{n+1}$ est vraie.
on a alors $P_n$ vraie pour tout entier naturel $n$.Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - En déduire les variations de la suite $(u_n)$.
Aide
On peut étudier le quotient $\dfrac{u_{n+1}}{u_n}$ car $u_n >0$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Montrer que $(u_n)$ est convergente et préciser sa limite.
Rappel cours
Limite d'une suite majorée ou minorée
Si la suite $(u_n)$ est croissante et majorée alors elle est convergente.
Si la suite $(u_n)$ est décroissante et minorée alors elle est convergenteSolution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message